My dissertation process - Individual Project

This is just going to be one of the places where I start to take down notes on what I have been doing in my individual project. It's been a tough ride up to now and I'm sure it will get more tough from here. First and foremost, the initial title I went with was as follows:

Simulating cancer immunotherapy using an eventually consistent distributed system.

I was super happy with this title because it covered a lot of what I wanted to do. Distributed systems is something I find interesting to this day. The topic of "cancer" intrigued me because I'd always thought about it as a disease that has some cause and we can find and cure it. If this project would help me even a tiny bit then I would absolutely love that. I've always had a curiosity in biology and the medical sciences too.

This all sounds great but I needed to make a start. I needed to find resources that would help me solve this issue. I wanted to do this step by step, in steps which I thought were calculated. I wanted to focus on the viability and the methodology of how I could simulate cancer immunotherapy. For this I started to read some papers online, I tried to find different ways in which I could address this problem. In doing this I came to two realisations:

1. This could turn out to be more of a Machine Learning paper rather than a distributed systems paper. I say this because the simulation requires handling multivariate data.
2. This was a bigger project than I had initially thought. Finding papers for it were difficult and there were different branches of knowledge I had to cover before attempting to understand some relevant papers. With this in mind, I needed to boil down the question to something I can do within my viable 6-7 month period.

Both of these realisations pointed to the same thing that I had to do. Remove distributed systems from the question (for now). With this my new title became:

Exploring different methods to simulate cancer immunotherapy

So that's where I went with it. I explored. I saw what was out there and thought about that. After a lot of research the first method became apparent - Ordinary Differential Equations (ODEs).

ODEs to simulate cancer immunotherapy

A paper I found, with title Modeling immunotherapy of the tumor – immune interaction, resembled somewhat the general "thing" that I wanted to do. Page 237 of this Journal had the following ordinary differential equations:

$$\frac{dE}{dt} = cT - \mu_2 E + \frac{p_1 E I_L}{g_1 + I_L} + s1$$ $$\frac{dT}{dt} = r_2 (T) T - \frac{aET}{g_2 + T}$$ $$\frac{dI_L}{dt} = \frac{p_2ET}{g_3 + T} - u_3 I_L + s_2$$

where $E$ is the number of effector cells i.e. the cells in your immune system that fend your body from any harmful pathogens, $T$ is the number of tumour cells and $I_L$ is the level of cytokines. The equation, initially is quite hard to understand and it contains a lot of different variables and constants so we're going to take equation in it's simple differential form. Each equation represent the growth or decline of Effector Cell, Tumour Cell and Cytokine levels.

"...the cells that orchestrate the immune response use cytokines as signaling mechanisms for immune-response stimulation as well as lymphocyte stimulation, growth and differentiation."

So, how do effector cells and cytokine work together?

Let's break down the answer. Into diagrams.

Step 1: Identifying Pathogens/Tumours

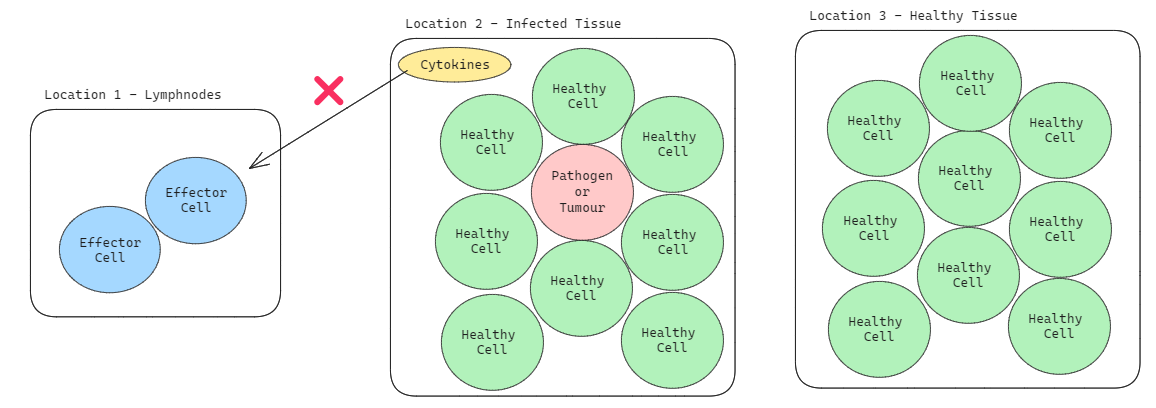
First, the cytokine (or $I_L$) is injected into the area with tumours. The presence of $I_L$ tells the Effector Cells that there is something wrong in that area and therefore, they must deal with it.

Step 2: Dealing with it

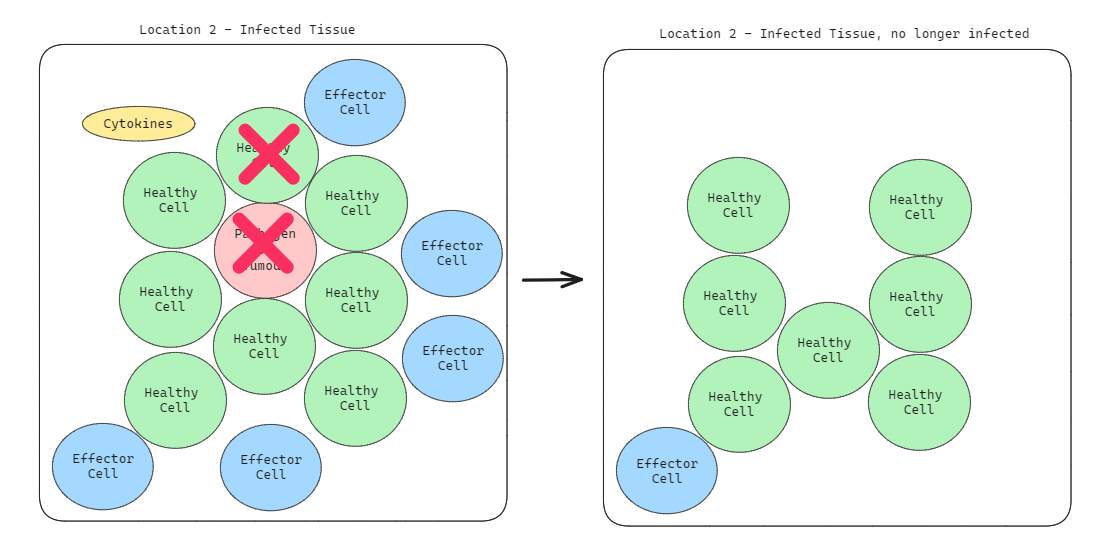As you can see in the left section of picture above, the effector cells divide and grow rapidly to combat this pathogen wherever the Cytokine is located (in this case Location 2). The location of the cytokines tell the effector cells the general area of which the pathogen is located. The effector cells then attack and destroy the pathogens (and potentially, some healthy cells in the process too, eek). After they're done, that location has no more unhealthy cells (as seen in the right section of picture above).

Okay, but now what do we do with the equation?

We use the equation, plug in some values, and see which one leads to the eradication of the tumour and which one leads to something else. Simple. Right? Not really. At the time of doing this, the first thought I had was - What are "some" values? The differential equation had a number of distinct variables that needed a specific value in order to calculate the growth rate. In no particular order, these were: $E_0$, $T_0$, $I_{L_0}$, $c$, $\mu_2$, $p_1$, $g_1$, $g_2$, $r_2$, $a$, $\mu_3$, $p_2$, $g_3$, $s_1$, $s_2$.

Fortunately enough, the same paper had some information as to what values should be fed into some of the variables.

However, this isn't enough. There is no indication for the values of $s_1$ and $s_2$ in this table. Upon further reading of the same paper, (on page 243) we find that:

1. The model (or the set of differential equations) considers either or both $s_1$ and $s_2$ to be non-zero.
2. $s_1$ represents the addition of LAK or TIL cells to the tumour site.
3. $s_2$ represents the addition of interleukin-2 (IL-2) to the tumour site.

(According to Wikipedia) Lymphokine-activated killer cell (LAK) is a white blood cell that has been stimulated to kill tumor cells. Tumor-infiltrating lymphocytes (TIL) are white blood cells that have left the bloodstream and migrated towards a tumor.